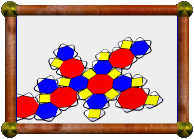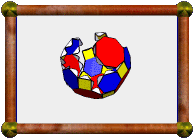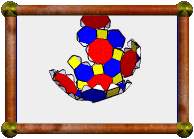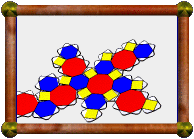
| 0.5 Cross-Section of Great Stellated 120-Cell |

The great stellated 120-cell is number 12 in the list of uniform polychora in
Stella4D,
with the abbreviated name "gishi". It is a regular polychoron, with 120
great stellated dodecahedra as its cells.
The model you see here is a 3D cross-section through that 4D polytope, taken
50% of the way through the model, along one of the 60 icosahedral symmetry
axes. The location of the slicing hyperplane has been chosen to pass through 30
of the polychoron's vertices. In
Stella4D,
use the yellow left and right arrows in the top right part of the cross-section
view to step through slices that coincide with vertices of the model.
See this tutorial for some comments on
obtaining nets for building paper models of 4D polytopes.

|
First, print out the nets. Initially Stella decided to pair these blue
parts differently. Still valid, but taking up more space. I used
Cut/Uncut Edges mode to force
their arrangement as you see here. A single cut will suffice to force
connection at the opposite edge.
|

|
Here are the three different types of net you need. Scored, cut,
folded and ready to go.
|

|
Start attaching pieces like this.
|

|
Here's what it looks like so far upside down.
|

|
Continue like this.
|

|
Here's half the model. At this point I put some extra parts inside to
add strength. Otherwise the final model will be too squishy and
flexible. The parts are pieces of decagrams. To create these
load a great dodecahemidodecahedron in Stella4D, with the
same radius as the model being built. Use
"Nets→Coincident Edge Method→No Internal Support Required" to
allow the decagram parts to combine into nets with 5 parts each, and
print a few of those, butchering them to get pieces of different size
to use to add strength. Cut them out without tabs, and without scoring
or folding, and glue them to the existing tabs inside the model. A
couple of spare parts can be seen here too, waiting to be glued inside.
|

|
Half the model again, right way up. It's hard to think how the last
part can be glued into this model. At this point I considered whether
to make two complete halves and glue them together, a technique I used
for the great icosidodecahedron,
but decided on another course that I thought more likely to yield
better results.
|

|
So I continued along, adding more pieces inside for strength as I went.
|

|
When reaching this point, take another net from the great
dodecahemidodecahedron, this time keeping the whole thing, scoring and
folding the edges, and leaving just one pair of tabs either end, gluing
the ends together to form a crown. Carefully glue this crown into the
remaining hole under the tabs around its perimeter.
|

|
The final part will sit snuggly in the above hole.
|

|
The final cap again, upside down. This part also needs a crown like
above glued under the tabs around its perimeter.
|

|
The cap should fit snuggly in the hole. Glue all around when you've
checked that it fits, and you're done!
|

|
Here's the model with the cap in place, but not yet glued. You can see
it fits quite well even before gluing. It was tempting to leave it as
a box with removable lid! Maybe something could be added to the base
of the cap so that it clips in unless some force is applied to open it.
Too late though for me, it's now glued forever in place!
|

|
Here are all four gishi cross-sections taken at hyperplanes
which pass through successive vertices of the polytope, built at
appropriate relative sizes:
|

|
And again with the city of Melbourne, Australia, as a backdrop.
|

|
Here's an animation of the gishi cross-section as the slicing
hyperplane moves through the model.
Can you spot the four cross-sections above?
|