| Stella Screenshots |
This page contains screenshots from
Small Stella,
Great Stella and
Stella4D.
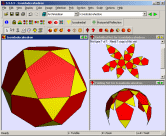
|
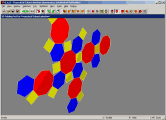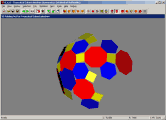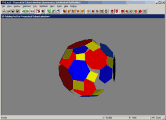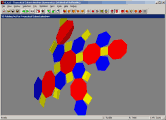
This screenshot is from
Small Stella, but could equally well
be from Great Stella or
Stella4D (except the toolbars would look a little different).
It shows a three-view layout. There are a number of layouts to choose
from, showing anywhere between one and six views at a time. Each view
may be one of many different types. Here we can see a view of a
uniform polyhedron (the icosidodecahedron in this case), a view of the
2D net required to build it, and a 3D view of the net folding up.
|
|
Here we see a single-view layout, showing a view where the net may be
folded up into the model using the mouse.
|
|
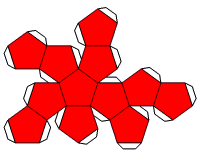
Tabs may be printed on nets. You may choose the single
tab method, as shown here, where only half the edges around nets
have tabs. Construct the model by gluing tabs under their connecting
faces.
|
|
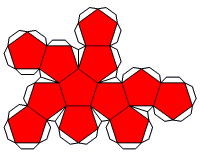
Or you may choose the double tab method, where all edges around
nets have tabs. Construct the model by gluing tabs to each other.
This is my recommended method. I recommend getting some tweezers too!
|
Images may be put on faces of polyhedra, and will appear on nets when
printed out. Images may be mapped individually on each face, as in first image
below, or projected through the model linearly, cylindrically, or spherically
as seen in the other images below. The first image below also shows spheres at
the vertices and cylinders along the edges, with golden spheres and wooden
edges.




|
Small Stella,
Great Stella and
Stella4D can all display the
rotational and reflective symmetries of any polyhedron.
|

|
Now you can select a rotational symmetry axis and pivot around it.
|

|
Stella has customisable animated transitions between models.
|

|
Stella allows you to create polyhedral slideshows called tours.
Each event may be animated (rotating, morphing, unfolding, slicing),
with animated transitions between each. This animation goes for 30
seconds. Watch full 80 second version with commentary on YouTube
below:
|
|
|
Here we see cross-sections of various polyhedra. The animation comes
from moving the slicing plane through the model over time, and can be
shown in real-time within the software
(Small Stella,
Great Stella or
Stella4D).
Top left shows cross-sections embedded in the cube. This helps to show
how these slices fit into the original model. Can you tell which
polyhedra are being sliced in the other images?
|
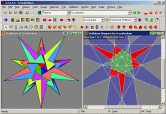
|
A screenshot from the Demo version of
Great Stella.
This shows the Rainbow colouring mode, and the fact that the
icosahedron may be stellated in the Demo
version.
|
|
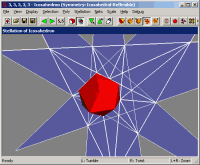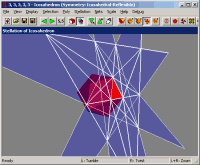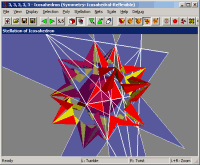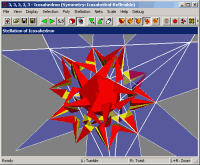
This is a screenshot from
Great Stella,
showing the stellation diagram attached to the face of a 3D model (the
icosahedron). The lines indicate
where other face planes intersect with this one. You can click on a
2D region of the diagram to enable the 3D cell behind that region,
as shown here.
|

|
In Great Stella,
use this toolbar button to enter "Create Facets Mode"...
|

|
...then use Shift+Left-click on the vertices of the
facets you want, which will become faces of a new model when you
use "Poly→Create Faceted Polyhedron". In this example we
create a compound of 15 cuboids. Only three facets need to be created
manually because they will be repeated over the symmetry group to
create the complete set of faces. Finally we colour them in orthogonal
sets of three using "Color→Special Color
Arrangements→Rhombic Triacontahedral Arr 1 (5 colors)".
|

|
Or, let Great Stella find facetings
for you. You can step through valid facetings, according to the
criteria you've selected, using the Up arrow in the
Faceting Preview view. Here are the facetings of the
icosahedron).
|

|
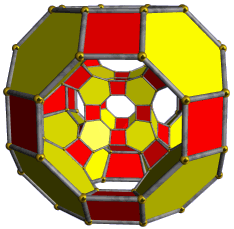
In Great Stella you can create a
zonohedron or zonish polyhedron based on any other
polyhedron. Here is a zonish polyhedron. Created as follows:
start with an icosidodecahedron, use "Poly→Zonohedrify",
select "Add zones to existing faces" at top, and tick only "All faces"
in the middle section.
|
|
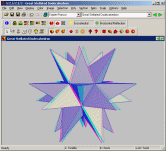
This screenshot is from Small Stella (and would also be available in
Great Stella and
Stella4D of course).
It shows a single-view layout, with 3D stereo enabled. You need to
wear red-blue or red-green glasses to view this image properly. Click
on the image for a full size version.
|
|
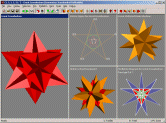
This screenshot is from
Great Stella.
It shows a five-view layout. The only view here that wouldn't be
available in
Small Stella is the one in the bottom right corner, which shows the stellation
diagram for the great icosahedron
in the big view. The model itself is available in
Small Stella.
Click image to see it full size.
|
|
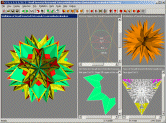
Another screenshot from
Great Stella,
showing the small inverted retrosnub icosicosidodecahedron (aka Yog
Sothoth). This model is only available in
Great Stella and
Stella4D.
Click image to see it full size.
|

|
This shows the augmentation feature of
Great Stella. You can augment any
model with any other model. Here a pentagonal pyramid (J2) is being
augmented with a square pyramid (J1) at one of the triangular faces.
The user sees a preview of the result and can cycle through the
possible orientations before choosing the one they want.
|

|
Measurement mode allows you to measure distance and angles between
points, lines, planes, and in Stella4D, cells.
|
|
Overlapping coplanar faces have their colours blended in real-time.
|
|
Formatted text may be places on faces, edges and vertices. Some
limited HTML markup is recognised in order to format and colour the
text. You may even have links in your text! Link to websites, email,
or to open other models in Stella.
|
|
Formatted text on faces is also printed on nets. Make your own
polyhedral dice.
|
Below are animations showing views where a polyhedron can be morphed into
its dual. Each shows a different model, and uses a different method for doing
the transformation. In the software, the transformation is controlled
interactively with the mouse. See
my paper for a description of
some of these techniques.
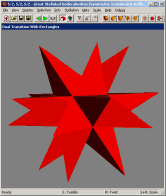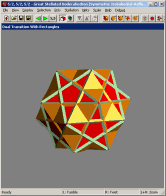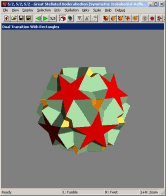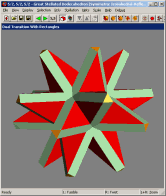

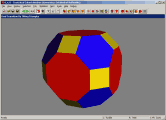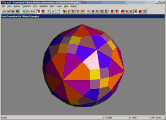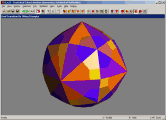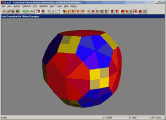

Enable Geomag mode to render models as if they were constructed using
the Geomag magnetic construction kit.
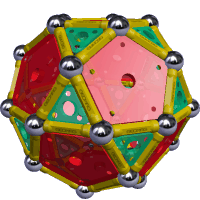 Geomag
Geomag
Icosadodecahedron
 Geomag rocket
Geomag rocket
 Geomag picture frame
Geomag picture frame
 Geomag castle
Geomag castle
Finally, let's have a look at some images created by
Stella4D. As a quick introduction to 4D, you
might want to read the first part of the 4D section in the Stella4D
manual.
|
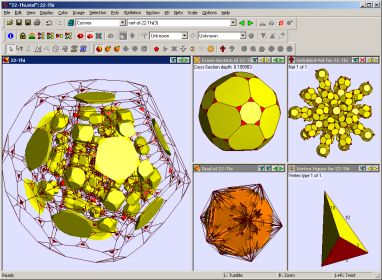
Screenshot from Stella4D (click image for full-size version). Shows the
uniform polychoron Thi, whose cells are 120 truncated dodecahedra and 600 tetrahedra. The smaller views show a
cross-section, net, dual, and vertex figure.
|
|
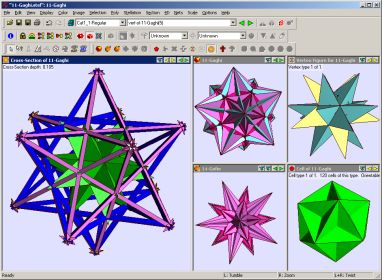
Screenshot from Stella4D (click image for full-size version). Shows the
regular polychoron Gaghi, whose cells are 120
great dodecahedra. The main window shows a 3D
cross-section of the polytope.
|

|
Here is the best known polychoron and probably the simplest to understand.
It is the tesseract, also known as the 8-cell or 4D cube. It has eight
cubes as its cells (or sides). Here it is shown with all the cells
hidden, leaving just the edges and vertices visible. It has been projected
into 3D so that we may view it in our world, just as a 3D model is
projected into 2D when we view it on a computer screen.
|
|
Getting a bit more complicated, here is a cantitruncated tesseract (uniform
polychoron number 308, aka "grit", in Stella4D). This polytope has 56
cells. 32 truncated cuboctahedra (hidden),
16 truncated tetrahedra (yellow), and 8
triangular prisms (red). Again, it has been projected into 3D, this time
with only the truncated cuboctahedral cells hidden.
See my paper model here.
|
|
|
Each "side" of a 4D polytope is a 3D polyhedron, just as each side of a
3D polyhedron is a 2D polygon; and just as in 3D, you can unfold the sides
into a "flat" net. I put "flat" in quotes because here flat means that the
unfolded cells lose their four-dimensionality, being reduced to 3D. Here
you see two such nets. The first for the truncated tesseract (19-Tat in
Stella4D. See my paper model). The second is for
the dual of another uniform polychoron (20-Thex).
|

|
Nets for more complex polychora get quite impressive. Here is the net for
the cantellated 120-cell (158-Srahi in Stella4D).
|
|
3D perspective projection of the 120-cell, a regular 4D polytope with
120 regular dodecahedra for its sides.
|
|
Net for a 7,2 gyrochoron. Gyrochora are duals of step prisms, so
use "4D→Create 4D Step Prism" in
Stella4D, enter "7 2" when prompted, and
look at the net of the dual to find this model.
|

|
Here is the tesseract rotating in 4D before being projected into 3D.
Stella4D lets you rotate like this
interactively.
|
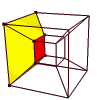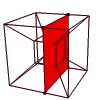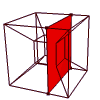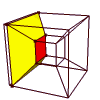
|
The tesseract again, with a cell-first cross-section passing through it.
The cross-section itself doesn't change, remaining a cube throughout, but
appears to distort due to the projection from 4D into 3D.
Stella4D lets you interactively change
the slicing depth with the mouse.
|

|
This time it's a vertex-first cross-section, which starts as a growing
tetrahedron, gets truncated towards an octahedron, then extends out the
other way back into a tetrahedron. Again, it appears distorted throughout
due to the perspective projection from 4D into 3D.
|

|
Here are cross-sections of the 600-cell, which has 600
tetrahedra as its sides. Not embedded in
the original 4D model here, so no distortion this time.
|

|
Cross-section of a 4D Waterman polychoron.
|

|
Getting more complex now, and this is still just a regular polychoron!
Here we see cross-sections of the great grand stellated 120-cell
(16-Gogishi in Stella4D), which has 120
great stellated dodecahedra as its cells.
|

|
Cross-sections of another regular polychoron, the great stellated 120-cell
(12-Gishi in Stella4D), which again has
120 great stellated dodecahedra as its
cells. I have made two of these cross-sections as paper models
here and
here.
|

|
Here's a cross-section of the grand 600-cell (15-Gax in
Stella4D), which has 600 tetrahedra as its cells.
|
|
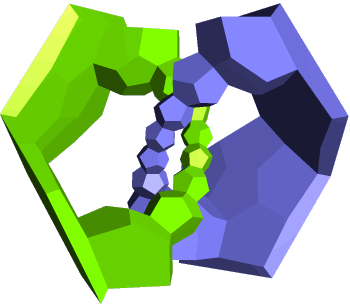
Here you see the 120-cell (5-Hi in Stella4D)
projected into 3D. Most cells have been hidden, with just two rings of
dodecahedra remaining.
Colour Mode makes it easy to recolour
each cell in a ring like this, then you can hide all the remaining cells of the
original colour in one hit.
Update: I have now made this model from paper, adding one extra cell
to hold the two rings in place.

|
 |
 |
Two methods are available for morphing between 4D polytopes and their duals.
|