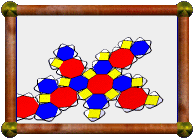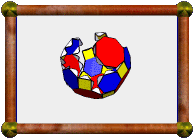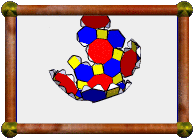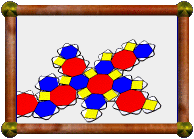
Great Icosidodecahedron

Like or comment on facebook

• Vertex description: 5/2.3.5/2.3
• Faces: 32
• Edges: 60
• Vertices: 30
• External facelets: 132
• Dual: Great rhombic triacontahedron

  This uniform polyhedron's faces consist of 20 triangles and 12 pentagrams. Can you spot them?

  The polyhedron can be thought of as a half-way point between the great stellated dodecahedron and its dual the great icosahedron. It's relationship to those regular polyhedra is the same as the icosidodecahedron's relationship to the dodecahedron and its dual the icosahedron. In both cases the uniform polyhedron can be found at the half-way point when morphing by truncation in Small Stella, Great Stella, or Stella4D.

  This is one of my favourite polyhedra!

  	After making about half of this model, using only the externally visible parts, I noticed it was quite flexible. I printed out some decagrams, matching in size to the decagram you get when you take a cross-section right through the centre of the model.
  	A number of decagram parts can be glued inside to the existing internal tabs. Finally I glued a whole decagram (with a hole in the middle to get tweezers through) under the free tabs around the rim of the first half of the model.

  Rather than figure out how to put the last part in, I made two complete halves of this model as described above. Then I just glued the two halves together. It's hard to tell where the join is now. I'm a bit surprised this worked so well!

  	You can see roughly how big the model is here.
  	Here is a very small version of the model made using SLA rapid prototyping, along with a model of its dual.

  Home > Gallery > My Models > Uniform Polyhedra > Great Icosidodecahedron
  Prev (Dodecadodecahedron)	Next (Great Dodecicosidodecahedron)