

| Home > Gallery > My Models > Stewart Toroids > A Genus-41 Stewart Toroid | |
| Prev (Cupola-Drilled Truncated Icosidodecahedron) | Next (Tetrahedral Stellation of Dodecahedron 1) |
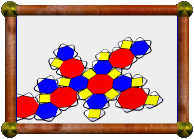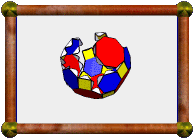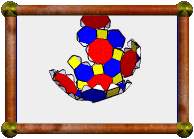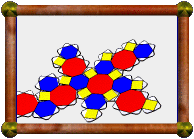
A Genus-41 Stewart Toroid |

| Like or comment on facebook |
This polyhedron is one I discovered myself, a new Stewart Toroid. B. M. Stewart explored these in Adventures Among the Toroids. In that book he explored polyhedra with non-intersecting regular faces and genus greater than zero (i.e. with holes), and proposed five criteria to help narrow the search. His preference was for polyhedra where each edge of the convex hull was also an edge of the polyhedron itself. This requirement sounds a bit arbitrary at first, but after playing around with it you get the idea, and it does generally lead to more aesthetically pleasing polyhedra. He noticed though that this requirement almost always meant that the faces of the convex hull were also regular, so he looked for examples where this wasn't the case.
He only came up with a couple of examples, but they weren't very satisfying, broke some of his other requirements, and had low symmetry. More recently, Alex Doskey discovered four new polyhedra which satisfied all the criteria and were much more in the spirit of other Stewart toroids, but whose convex hulls had some irregular faces. Just what Stewart was looking for (click here for one such model). They all had octahedral symmetry. This prompted me to look for more, and in particular, to see if I could find examples with icosahedral symmetry. I did find four more examples with octahedral symmetry, as well as four new examples with icosahedral symmetry (including the one shown above). They are all available in Great Stella's polyhedron library (the one shown here is Stella Library > More Stewart Toroids > 12(J6-Q5S5) + 20J63 + 60S5 + 60P5, a rather complicated name that describes what the components are and how they are put together).
Here are the other ones I discovered
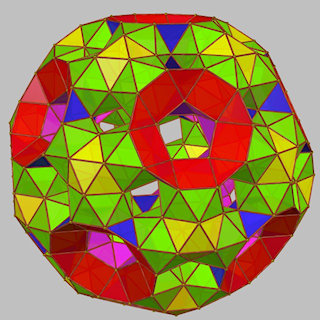
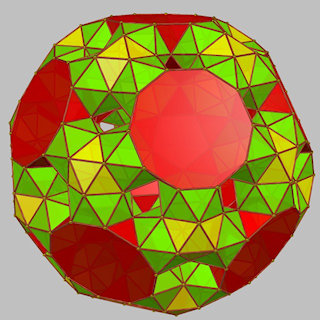

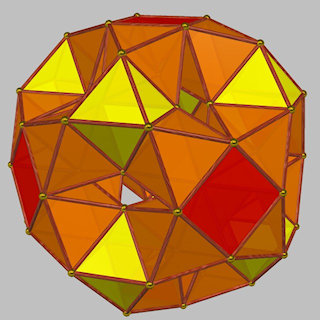
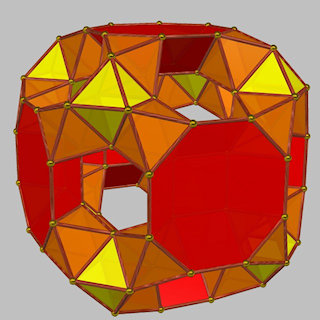

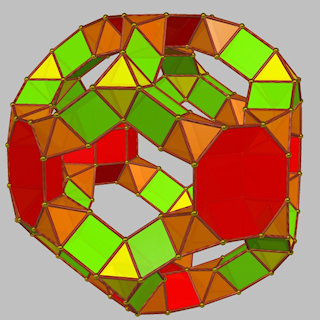
The basic icosahedral forms can either have their decagonal faces drilled (with a pentagonal cupola / pentagonal antiprism combo) or not, giving rise to many more toroids with lower symmetry by combining these in different ways.
This toroid is also physically the largest known, relative to edge length, of the toroids satisfying all of Stewart's criteria.
Its genus of 41 is not quite up to Stewart's previous record of 46, but it can be augmented internally to increase the genus. The hollow interior is large enough that the previous record breaker can be entirely fitted inside it. The 46 genus model has hexagonal faces on the exterior, one of which can be augmented with a triangular cupola (J3), whose opposite triangle can then be attached to the interior of the new model presented here. This leads to a toroid with the new record genus of 87.

|
This is the convex hull of the model. You can see that some of the faces (the yellow dodecagons) are not quite regular. All edges are equal length however, and are also edges of the toroid, as required by Stewart. This convex hull makes quite a nice near miss (almost a Johnson solid). | ||

|
This diagram shows the convex components involved, augmented and excavated from each other, as listed in the notation 12(J6 / Q5S5) + 20J63 + 60S5 + 60P5. Their colours match the finished model. The S5 Q5 stack in the top right corner is subtracted from J6. | ||

|
Two types of component need to be made. Here are the nets for the first one. | ||

|
Start construction like this. | ||

|
Then attach the outer part around it. | ||

|
Here's two of the first component completed. This little model is itself a valid Stewart Toroid. | ||

|
Nets for the second component. | ||

|
I started like this. | ||

|
Wrap it around to close it up, just leaving a pentagonal hole at one end. The yellow section can then be attached. | ||

|
Attach a second silver/green part, made the same way as the first. After this, it's easier to add the next green part, and then the final silver part, rather than attaching them as a single finished unit. | ||

|
Two of the second component completed. | ||

|
All the parts in various stages of completion. You need 12 of the first component and 20 of the second. | ||

|
All parts finished and ready to assemble. | ||

|
It's fairly easy to assemble the parts. It involves gluing pentagonal faces to other pentagonal faces. | ||

|
Bit under half done. | ||

|
About half done. | ||

|
Mostly done. There were a few alignment issues and parts trying to pull apart, but be patient and you'll get there. | ||

|
Before finishing, you can wear it as a hat. | ||

|
Close-up of the finished model. | ||

|
Close-up of the finished model. | ||

|
Close-up interior of the model. | ||

|
3D-printed model. This model was made using SLA rapid prototyping,
using an OBJ file exported from Great Stella.
|
||

|
Close-up of the 3D-printed model. | ||

|
The 3D-printed model is only about 10cm across. You can see its size here. |
| Home > Gallery > My Models > Stewart Toroids > A Genus-41 Stewart Toroid | |
| Prev (Cupola-Drilled Truncated Icosidodecahedron) | Next (Tetrahedral Stellation of Dodecahedron 1) |