| Stellated Truncated Hexahedron |

- Vertex description: 8/3.8/3.3
- Faces: 14
- Edges: 36
- Vertices: 24
- External facelets: 54
- Dual: Great triakisoctahedron
- Name breakdown:
- Stellated: Stellate a cube. The cube has
no finite stellations, but one can add an infinite stellation cell to each
side.
- Truncated: Truncate the result with planes parallel to the faces
of an octahedron.
- Hexahedron: The cube, a.k.a. hexahedron, we started with.
Also known as the quasitruncated hexahedron, the intersecting faces consist
of 6 regular 8/3 octagrams in red, and 8 equilateral triangles in yellow. This
polyhedron is a faceting of the
rhombicuboctahedron, but not a true
stellation of the uniform truncated cube, the core
being a nonuniform version. It can also be created by truncating a cube
further than usual, back past the other end of each edge, if you can picture
that! This is what quasitruncated refers to.

|
These two nets get you started, and look like the normal nets you
would get for this model. I wanted a nice solid model though, so I
didn't quite just use the default nets.
|

|
Here you see the above parts put together, plus a part that fits at the
base. The default nets produced by
Great Stella
would only have made the small square in the middle. However, before
printing out nets, I deselected all the cells of the stellation that
comprise the inner cube, leaving the model with holes right through it
where those little squares should be.
|

|
The only difference this made to the nets produced was that now the
whole square base of each part was printed out, with the small square
still printed in the middle, intended as a hole to cut out. Instead
I glued the whole square base onto each part. The small printed square
is convenient for lining up the edges meeting around it (from the
yellow part).
|

|
The parts are then assembled as a cube would be. This method makes a
very rigid model.
|

|
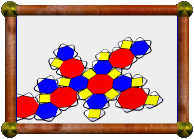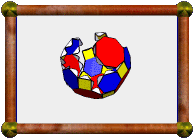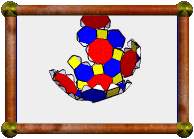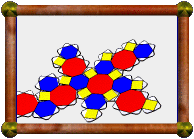
The finished model.
|