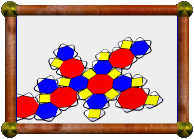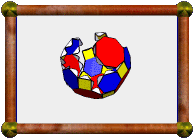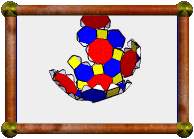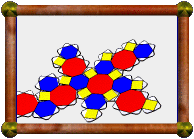
Great Stellated Truncated Dodecahedron

Dual of the great triakisicosahedron. Two decagrams (red) and one triangle (yellow) meet at each vertex.

	Twenty copies of these two nets are required to complete the model.
	An extra triangle is glued into the base of each part to add strength.
	The parts are then joined like an icosahedron.

Home > Gallery > My Models > Uniform Polyhedra > Great Stellated Truncated Dodecahedron.
Prev (Cubitruncated Cuboctahedron)	Next (Great Rhombicuboctahedron)