Great Rhombicuboctahedron

Like or comment on facebook

• Vertex description: 4.3/2.4.4
• Faces: 26
• Edges: 48
• Vertices: 24
• External facelets: 488
• Dual: Great strombic icositetrahedron
• Name breakdown:
  • Great: To distinguish polyhedra that would otherwise have the same name.
  • Rhombi-: 12 faces (squares) lie parallel to those of a rhombic dodecahedron
  • -cub-: 6 more faces (squares) lie parallel to those of a cube
  • -octa-: 8 faces (triangles) lie parallel to those of an octahedron

A uniform polyhedron whose faces consist of 18 squares (12 red, 6 blue) and 8 triangles (yellow). It is a faceting of the truncated cube, that is, it shares the same vertices. It also shares the same vertices with the great Cubicuboctahedron and the great rhombihexahedron. In fact all but the truncated cube share the same edges too.

Three squares and one triangle meet at each vertex. The squares come in two colours, as they fit into the model in two distinct ways. The six blue squares are in planes parallel to the faces of a cube, while the twelve red squares lie in planes parallel to the faces of a rhombic dodecahedron.

The description above also applies to the rhombicuboctahedron (with different colours). The two models are isomorphic since they share the same topology.

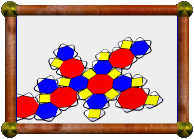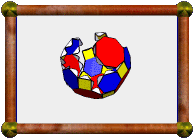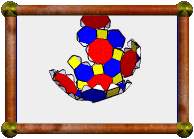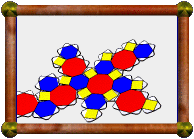
	There's a bit of work required to build this model. It has 488 external facelets, and 876 external edgelets. Great Stella helps by joining facelets into nets, and each join saves you having to score, fold and glue an edge. Shown here is one of the octagram parts completed.
	Here is the same octagram part upside-down. Basically you make six of these and then put all the remaining pieces together as you would the great cubicuboctahedron.
	Here the model starts to take shape, with two octagram parts and a few connecting pieces in place.
	Various parts inside can be glued together to add strength. The tips of the deepest recesses of the octagram parts touch each other between neighbouring parts, and so the tabs at their ends may be glued together (you might want to click on the image for a closer look). The octagram parts themselves are also quite floppy, so I have glued rectangles to the already-glued double tabs along the sides of the inner square of yellow edges. This keeps things in place quite well.
	Also, there are parts of the model which touch each other only along an edge. I have used Great Stella's "Internal Support" option from the "Nets>Coincident Edge Method" sub-menu (which is the default) when generating these nets, which results in there being a glued double tab on one side of these edges, and no tab (just a fold in the net) on the other side. If you look at the upside-down octagram part above, you can see that the outer radiating ridges alternate between tab and no tab. These double tabs are then glued to the back of the face from the touching net.
	Now for putting those last pieces in! The final octagram part should be completed on its own before putting it in place. The good thing is that you can still fold it up along those yellow edges, due to the way I strengthened them. I suggest putting all the blue corner pieces in, but leaving off the yellow double-triangle parts till the end. Here the final octagram part has been glued to one of the blue corner pieces, and is folded up along one of those yellow edges.
	Now the lid is closed, and each of the final three sections can be folded down and glued in place.
	Before gluing those final sections down though, I reached in with tweezers to glue those neighbouring deep octagram recesses together (you can just see it in the dark in there!). Finally the last four yellow double-triangle parts can be glued in place.
	This model fitted together surprisingly well in the end, and you'd never be able to tell which bit went in last (even I can't!). Here we see the completed model, standing on one of its 3-fold symmetry axes. Looking at the model, you wouldn't really think of it being able to stand this way, but it does!
	The view down a 4-fold rotational symmetry axes.
	The view down a 3-fold rotational symmetry axes.
	The view down a 2-fold rotational symmetry axes.
	This shows how big the model is. It has an edge length (or height, when sitting on its 4-fold axis) of about 14.5 cms.

Home > Gallery > My Models > Uniform Polyhedra > Great Rhombicuboctahedron
Prev (Great Cubicuboctahedron)	Next (Pseudo Great Rhombicuboctahedron)