Great Icosicosidodecahedron

Like or comment on facebook

• Vertex description: 6.3/2.6.5
• Faces: 52
• Edges: 120
• Vertices: 60
• External facelets: 1232
• Dual: Great icosacronic hexecontahedron

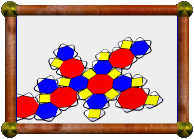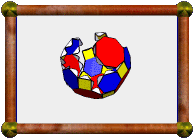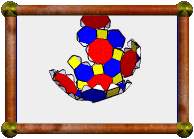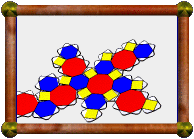
This model has 1232 external facelets to put together! It's a uniform polyhedron, and so all the faces are regular, but intersecting. Can you pick them out?! Each vertex is met by four faces, a triangle, a hexagon, a pentagon, and finally another hexagon which crosses back through the first one. Triangles and pentagons are not too hard to see, in yellow and blue respectively, but the red hexagons are harder to identify, with different parts of the hexagon visible from above and below.

This polyhedron is a faceting of the truncated dodecahedron (meaning they share the same vertex positions), and also shares its vertex arrangement with two other uniform polyhedra, the great ditrigonal dodecicosidodecahedron, and the great dodecicosahedron.

More than two months passed while making this model, but I was also working on many other things during that time, so it could be made faster. The completed model is very robust. It has an edge length of 14.5 centimetres, and a diameter of almost 33 centimetres.

My half-finished model even made a guest appearance on Australia's Today Show!

	Here's one of the nets printed by Great Stella, showing 10 red parts combined together.
	Put all these little pieces together from the nets, then glue them to each other.
	You now have the flowery part seen here. Its outline is a regular 10/3 decagram. 12 of these are required.
	This is the same part upside-down. Inside the 10/3 decagram is a 10/2 decagram, ie two overlapping pentagons. One of the pentagons has yellow edges. To add strength, I glued extra rectangles along the back of these yellow edges. Glued to three consecutive existing tabs, that is.
	These blue cups are then attached around the flower part. Then another flower part can be added and so on. There is also a pair of yellow triangles to go between each flower part, but I recommend you glue this in place after the two flower parts have already been attached. It's easier that way.
	Keep adding parts together! It may be hard to see in this picture, but behind each yellow triangle-pair are small tabs from adjacent flower parts that may also be glued together.
	Time for the infamous last part. Since I reinforced behind the yellow edges, you can still flex the flower parts along those edges. Here we see the last flower part being attached. It is first attached to one of the blue cups, and since the flower can be folded along the yellow edge, tweezers can still get in to secure these first tabs. Then continue gluing for the remaining blue cups. Tweezers can't get in now, but it still holds well. You can cut the hook off a coat hanger and use it to reach inside and check that the tabs are together.
	Finally glue the last five yellow triangle-pairs in place. Here's the completed model viewed down a 5-fold rotational symmetry axes.
	The view down a 3-fold rotational symmetry axes.
	The view down a 2-fold rotational symmetry axes.

Home > Gallery > My Models > Uniform Polyhedra > Great Icosicosidodecahedron
Prev (Great Rhombicosidodecahedron)	Next (Small Snub Icosicosidodecahedron)