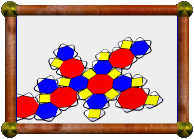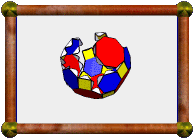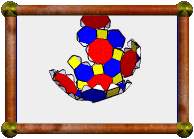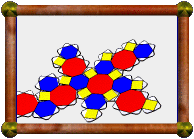
| Compound of 4 Cubes (Bakos' Compound) |

Known as Bakos' compound, this is a compound of 4
cubes.
To obtain this compound, imagine starting with 4 coincident cubes, then rotate
each one 60 degrees around a different 3-fold symmetry axis (the axes through
opposite vertices, top inset picture above). Since this leaves two opposite
vertices at the same position in each cube, you can still see all 8 vertices of
the original cube in the final compound (bottom inset picture).
This model is provided in
Great Stella's
Polyhedron Library. Its dual is a compound of 4 octahedra.
|
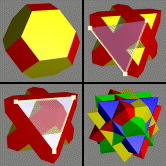
Here's a surprising way to create this model. Start with the
truncated octahedron (shown top left). Change
to a view of the stellation and hit the Up-arrow twice to get
the stellation shown here (top right). Enter Create Facets Mode
and create the two facets shown (top right and bottom left). Use
"Poly>Create Faceted Polyhedron" to create the compound of
4 octahedra (bottom right). "Color>Color as a Compound"
can be used to render each octahedron in its own color. Then the dual
of this model is the 4-cube compound. The reason this works is that
the dual compound of 4 octahedra requires 4 initially aligned octahedra
to be each rotated 60 degrees around axes through opposite faces, so
two triangles of each octahedron are rotated within their original
planes. This is what's happening when we go to the truncated
octahedron. The hexagons can be surrounded by triangles in two ways.
One way gives the original faces of a single octahedron. The other way
gives us one of the faces of the 4 octahedron compound. Stellation is
just a convenient way to access the new vertices required for these
rotated triangles, and then faceting allows us to connect the remaining
triangles.
|