Icosahedron

• Vertex description: 3.3.3.3.3
• Faces: 20
• Edges: 30
• Vertices: 12
• Dual: Dodecahedron
• Stellations:
  • Fully supported: 18 (16 reflexible, 2 chiral)
  • Miller's rules: 59 (32 reflexible, 27 chiral)

One of the five regular convex polyhedra known as the Platonic solids. This model was made from a single connected net, printed on one sheet of A4 paper. Nets can be generated and printed at any size using any of Small Stella, Great Stella, or Stella4D, even in the free demo versions.

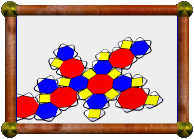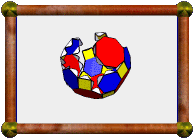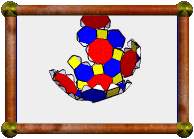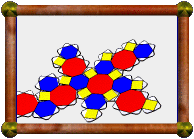
Above is an icosahedron with images of fractals on each face (seen from above, below, and in original net form). Stella allows you to map images onto faces in 3D. The images then appear on nets when you print them out, ready to be cut out, folded up, and glued together as seen here.

The fractal images were created using another piece of software I wrote. It is not yet available for sale, but let me know if you are interested and I'll notify you if it ever becomes available.

Here's an icosahedron in Stella, using a 3-view layout featuring the icosahedron itself, the unfolded net, and a partially folded net. See more screenshots here.

	Here is a compound of the icosahedron with its dual. Notice how the dodecahedron's vertices sit above the icosahedron's faces, and vice versa? Also the edges of the two polyhedra bisect each other at right-angles.
	The icosahedron has quite a few stellations. Here is one example.
	Here's another stellation.
	And another stellation, the medial triambic icosahedron (or the great triambic icosahedron, as they look the same).
	This is the final stellation of the icosahedron, meaning that if the facial planes are extended farther, they will never again close off another volume of space.
	A few famous compounds are to be found among the stellations, such as the 5 octahedra shown here.
	The compound of 5 tetrahedra is another well-known stellation.
	The compound of 10 tetrahedra is yet another stellation.
	Perhaps the best known stellation is the great icosahedron, one of the four nonconvex regular polyhedra known as the Kepler-Poinsot solids. In this case, it is not just a stellation of the icosahedron, but also a faceting of it, meaning it shares the same vertices, as you should be able to see.
	The small stellated dodecahedron is also a faceting of the icosahedron, though it is more commonly thought of as a stellation of the dodecahedron.
	In fact three of the four Kepler-Poinsot solids are facetings of the icosahedron. Here is the third, the great dodecahedron. This too is more commonly thought of as a stellation of the dodecahedron.

Home > Gallery > My Models > Platonic Solids > Icosahedron
Prev (Dodecahedron)	Next (Truncated Tetrahedron)