Home > Gallery > My Models > Cupolae > Crossed Pentagonal Cuploid
Prev (Crossed Pentagrammic Cupola)	Next (Topological Small Stellated Dodecahedron)

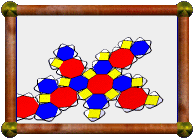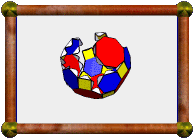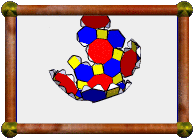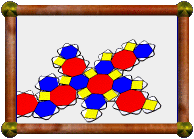
Crossed Pentagonal Cuploid

Cuploids are similar to cupolae, but the n/d-gon at the top must have an even value for d. This means that the base is a 2n/d-gon, but since the top and bottom are both even now, we get two coincident n/(d/2)-gons instead. Each coincident edge meets a triangle for one of the polygons, and a square for the other, meaning a total of four faces meet at these edges. Polyhedronists generally don't like polyhedra with more than two faces at an edge. By removing the two coincident base polygons and letting the triangles connect to the squares instead we get back to a more acceptable two-face-per-edge model.

The model presented here is a 5/4 cuploid. It's upside-down in this photo with respect to the description above (the 5/4-gon is at the bottom instead of the top). A 5/4-gon is a retrograde pentagon, ie a normal pentagon, but we visit the vertices in the opposite order. The base would be a 10/4-gon, which is two coincident 5/2-gons. These coincident base pentagrams have been removed as described above, but you can see the outline still there, now with triangles meeting squares at these edges instead.

Home > Gallery > My Models > Cupolae > Crossed Pentagonal Cuploid
Prev (Crossed Pentagrammic Cupola)	Next (Topological Small Stellated Dodecahedron)