Page 1 of 1
Nadia's Icosahedron
Posted: Sat Sep 22, 2018 5:52 pm
by sicherman
Donald Bell has written up a polyhedron discovered by a young visitor to his home. He calls it Nadia's Icosahedron.
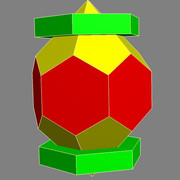
It has a girdle of six regular hexagonal faces, non-regular pentagons in the angles between the hexagons on both sides of the ring, and a regular hexagon at each end. Bell has worked out all the sides and angles. He has also shown that 3-space can be packed with copies of Nadia's icosahedron and an enneahedron that he has also analyzed.
I suspect that the enneahedron is this "Associahedron" as shown at the bottom of this page:
http://www.orchidpalms.com/polyhedra/ac ... ss/554.htm
And the icosahedron itself looks much like Robert Webb's polyhedron at the bottom of this page:
http://www.orchidpalms.com/polyhedra/ac ... ss/554.htm
The main difference is that the depressed pyramids around the girth must be replaced with hexagons, and the dimensions of the pentagons must be adjusted accordingly.
Bell would like to know whether anyone has previously discovered Nadia's Icosahedron. (So would I.)
Re: Nadia's Icosahedron
Posted: Sun Sep 23, 2018 6:35 am
by robertw
Looks like you accidentally gave the same link twice, so I'm not sure which of my polyhedra you were referring to.
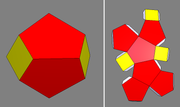
Here's my attempt at Nadia's icosahedron (it's a bit more distorted than it should need to be)
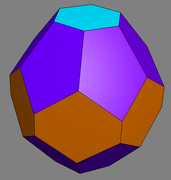
I believe you're right about the enneahedron that would complete the tesselation.
I don't know if it's been described before.
Re: Nadia's Icosahedron
Posted: Sun Sep 23, 2018 11:48 am
by sicherman
How pretty! Thank you for your reply. I will forward it to Donald Bell.
Re: Nadia's Icosahedron
Posted: Sun Sep 23, 2018 3:24 pm
by robertw
Actually, this might be a nicer version. This one has all regular hexagons and they're all the same size. The pentagons can't be regular though.
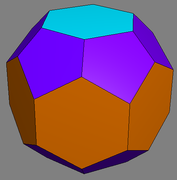
Re: Nadia's Icosahedron
Posted: Sun Sep 23, 2018 4:25 pm
by sicherman
This is exactly what Donald describd! May I forward your picture to him and a few other interested mathematicians?
Re: Nadia's Icosahedron
Posted: Mon Sep 24, 2018 2:58 am
by robertw
Sure, feel free to forward it.
Here it is with Stella showing it's net folded up slightly:
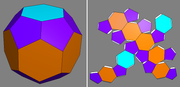
Here it is after gluing a few together:
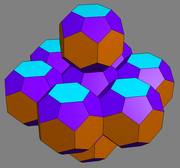
After sticking 8 together you can use Faceting mode to create the enneahedron
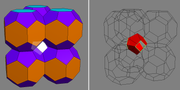
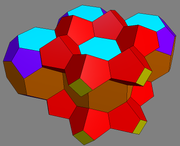
And here's the final enneahedron:
Then you can easily glue the various pieces together in Stella:
For Stella users, here are the two .stel files:
https://www.software3d.com/StelFiles/Na ... edron.stel
https://www.software3d.com/StelFiles/Na ... edron.stel
Re: Nadia's Icosahedron
Posted: Mon Sep 24, 2018 2:29 pm
by sicherman
This is beautiful work. I have forwarded your drawings to my correspondents, giving credit to you and Stella.
Re: Nadia's Icosahedron
Posted: Mon Sep 24, 2018 4:34 pm
by Ulrich
Robert,
Beautiful work! I tried to get it on my own but i could not make the hexagons regular. The best result gave the „create spring model“ tool. In the lateral hexagons there is a difference in the long diagonals of about 2% and the top/bottom hexagons are regular but have a different edge length.
How did you do that?
Ulrich
Re: Nadia's Icosahedron
Posted: Mon Sep 24, 2018 6:41 pm
by Ulrich
I‘m on my way, got the lateral hexagons regular. I made a model of these hexagons and triangles only which can be trimmed with the „try to make faces regular“ tool.Then I took the convex null and expanded the remaining triangles to kites.
Now what is the trick to cut down the top and bottom vertices to the correct depth so that the edge length of the resulting hexagons is the same as that of the others?
Ulrich
Re: Nadia's Icosahedron
Posted: Mon Sep 24, 2018 7:34 pm
by sicherman
Donald Bell's draft document includes all his calculations of the shapes. I cannot attach it here, but for a limited time you can download it from my website:
https://userpages.monmouth.com/~colonel ... hedron.pdf
Re: Nadia's Icosahedron
Posted: Tue Sep 25, 2018 8:51 am
by Ulrich
Thank you very much, I got it. And I found out how to construct the desired shape with stella:
The half of the top angle of the pyramid on the top/Bottom face is 45° and the height is the same as the bottom edge. So I have to construct a frustum of that pyramid so that the top edges are the same as in the lateral hexagons of the base model. It is the case if the height of that frustum is 2/3 of the pyramid's height. This can be done with prisms trimmed to that height:
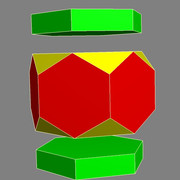
I found that Roger Kaufman (
http://www.interocitors.com/polyhedra/ ) already constructed such an icosahedron. In March 2017 he presented a list of more than 130,000 fullerenes. There, in the fg36-regiment it is listed in the D6h-symmetry folder. But he doesn't have all hexagons the same size.
Re: Nadia's Icosahedron
Posted: Tue Sep 25, 2018 1:51 pm
by sicherman
Thanks for working this out. I was not aware of Kaufman's work.
I have forwarded your analysis to Donald and the others.
Re: Nadia's Icosahedron
Posted: Wed Sep 26, 2018 12:49 pm
by robertw
Well done Ulrich. I didn't even follow what you did really but that's OK

To get the hexagons regular, the usual "Poly->Try to Make Faces Regular" doesn't work because they can't all be regular.
Instead, use "Poly->Create Spring Model". Tick the "Start with original vertices" box and add "~5" at the start of the text. This means to allow near-miss faces for polygons with up to 5 sides. And bam it works.
It's a bit of a blunt instrument because your near-miss faces have to be up to a certain size. In the future I'll make this more flexible.
Re: Nadia's Icosahedron
Posted: Fri Sep 28, 2018 7:03 am
by Ulrich
Ah, thanks! I tried ~6 but that could not work, as I know now.
Ulrich








