Hi Rob,
Long time no see. Off and on I have been working on the underlying theory of polytopes, with a view to applying it to stellations and facetings. Now that I have at last got there, I am interested in enumerating the facetings of the regular dodecahedon in particular. (I published its faceting diagram along with several others a good many years ago, in the Mathematical Gazette).
Your current info on Great Stella says that users can step through the allowed facetings, according to the rules selected. Are these just the rules for the dual stellations, or have you developed a set of rules directly applicable to facetings? Is there such a thing as a count of the permitted facetings, other than the count of the permitted stellation cell sets? This is particularly relevant, as some distinct facetings yield the identical cell set for the dual stellation.
Facetings of a polyhedron
Facetings of a polyhedron
Cheers,
Guy. Guy's polyhedra pages
Guy. Guy's polyhedra pages
- robertw
- Site Admin
- Posts: 721
- Joined: Thu Jan 10, 2008 6:47 am
- Location: Melbourne, Australia
- Contact:
Re: Facetings of a polyhedron
Hi Guy,
No the faceting criteria are not related to the stellation criteria at all. It's all specific to faceting. It finds all possible facets, and then enumerates valid combinations of them.
The available criteria can be see in the menu below. I think "tidy" facetings may have been your term?
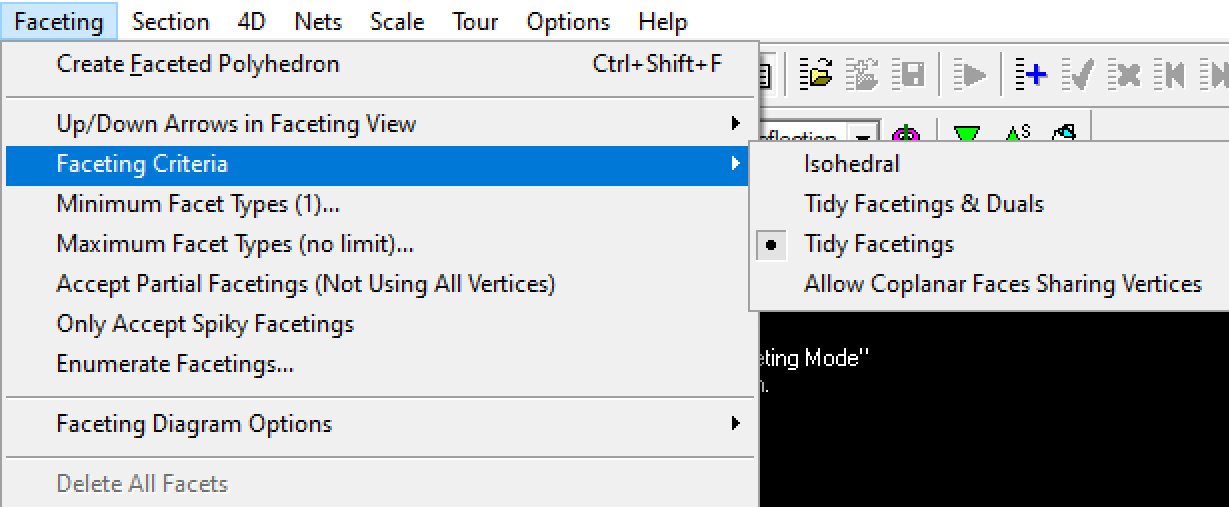
For the dodecahedron, I get the following results:
No the faceting criteria are not related to the stellation criteria at all. It's all specific to faceting. It finds all possible facets, and then enumerates valid combinations of them.
The available criteria can be see in the menu below. I think "tidy" facetings may have been your term?

For the dodecahedron, I get the following results:
- Tidy Facetings - 24 facetings, which includes 1 chiral and one compound of two chiral halves
- Tidy Facetings and Duals - 22 facetings, which includes 1 chiral and one compound of two chiral halves
Re: Facetings of a polyhedron
Thank you.
There seems to be a more or less "unlimited" option in there, excellent. Now I just need to get to grips with WINE.
Yes, "tidy" is a term I introduced, but the whole point of it is that it has no rigorous definition - it is a rag-bag of intuitive notions, which sometimes lead to paradoxes. I have since found out that abstract polytope theory has the equivalent term "faithful", as in a faithful realization of the abstract structure (It wasn't meant to be an intuitive mess, but it turned out that way; abstract theorists found that they differed significantly among themselves, on their criteria for faithfulness).
There seems to be a more or less "unlimited" option in there, excellent. Now I just need to get to grips with WINE.
Yes, "tidy" is a term I introduced, but the whole point of it is that it has no rigorous definition - it is a rag-bag of intuitive notions, which sometimes lead to paradoxes. I have since found out that abstract polytope theory has the equivalent term "faithful", as in a faithful realization of the abstract structure (It wasn't meant to be an intuitive mess, but it turned out that way; abstract theorists found that they differed significantly among themselves, on their criteria for faithfulness).
Cheers,
Guy. Guy's polyhedra pages
Guy. Guy's polyhedra pages
