 |
 |
 |
| Home > Gallery > My Models > Uniform Polyhedra and their duals | |
| Prev (Prisms and Antiprisms) | Next (Stellated Polyhedra) |
Uniform Polyhedra and their Duals |

A uniform polyhedron may be completely specified by its vertex description, which describes the sequence of faces around each vertex. For example, 8.8.3 indicates a truncated cube, because each vertex is surrounded by two regular octagons and an equilateral triangle. Some uniform polyhedra also make use of nonconvex regular polygons, such as pentagrams. A regular pentagram (5-pointed star) is described as 5/2, meaning that its 5 sides go around the polygon's centre twice before repeating. Uniform polyhedra make use of pentagrams (5/2), octagrams (8/3) and decagrams (10/3) in addition to other convex regular polygons. One such example is 8/3.3.8/3.4 which specifies the great cubicuboctahedron, having a cycle of faces around each vertex as follows: a regular octagram, equilateral triangle, another octagram, and a square.
These models were made using nets generated by Great Stella and can also be made using Stella4D. When you load a uniform polyhedron in Stella, it is generated on-the-fly just from the vertex description. That is, the final geometry is NOT already stored anywhere in the program.
Click on the images below to see a bigger picture and find more photos and information about them.
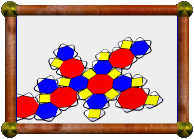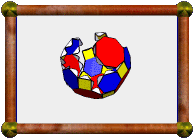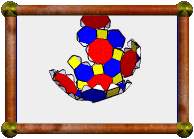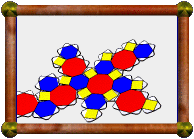
Uniform Polyhedra























Duals of Uniform Polyhedra








| Home > Gallery > My Models > Uniform Polyhedra and their duals | |
| Prev (Prisms and Antiprisms) | Next (Stellated Polyhedra) |
|
|
|
See all my products at: http://www.software3d.com Copyright © 2001-2025, Robert Webb |
|
|