|
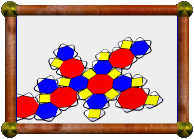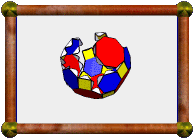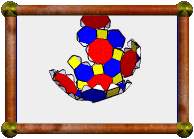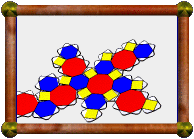
Here is one of the three cubes, together with the central
rhombicuboctahedron. You can see the cube has been rotated around a
horizontal axis 45 degrees relative to the symmetry of the
rhombicuboctahedron. This image matches the orientation of the main
photo above.
|

|
As well as being as stellation of the rhombicuboctahedron, here is
another unexpected method of construction. Augment a cube with
pyramids to get the model shown here (left) and its dual (right).
|

|
Enter Create Facets Mode and create two facets of this dual
model as shown. Then use "Poly→Create Faceted Polyhedron"
to create the 3-cube compound. Finally use
"Color→Color as a Compound" to color each of the three
cubes in its own color.
|

|
There are two kinds of net required for most of the model, one with two
facelets, and one with three (each net being a single colour). Near the
end though you often need to do things a little differently to be able
to get the last piece in nicely. A good idea is to always print out an
extra copy of each net, so that you can butcher them into smaller parts
later if necessary. Here you can see a special part I made near the
end to help finish the model.
|

|
Here the final special part is glued in place, and then just two flaps
remain to be closed. The trick is to try to be left with only convex
edges to glue at the end, because they glue more easily when you can no
longer reach inside with the tweezers.
|